I suspect that part of the problem is students fail to see meaning in the mathematics they study. However, I think this too is only part of the problem. When I was in high school I dissected an earthworm in biology and learned to do a backflip on a trampoline in P.E. Yet I have never relied upon my dissection skills to provide my wages, nor had to perform a backflip during a job interview. Yet I enjoyed learning both those skills, and I can’t remember any of my classmates asking, “When are we ever gonna use this?”
I suspect that the word “meaning” is not limited to utility and purpose. It is also connected to satisfying our brain’s natural and insatiable curiosity. When our brain is happy, we are connected to and engaged in our task.
This is what meaning is. We put more effort into work that we find meaningful, and we disconnect from work we perceive as meaningless. Meaningful work is significant to us.
Most likely, students disengage in a math classroom because unlike history, the people in the word problems aren’t real. In fact, most of the problems have no people or setting at all. Unlike P.E., math is often not kinesthetic and physically engaging. Unlike a story in a language arts class, math may not be entertaining to the typical student.
One typical math text applied the Pythagorean theorem by describing a student who measured the height of the ladder on a playground slide and the distance from the base of the ladder to the base of the slide ramp. The question then asked how long was the ramp of the slide. Though Pythagoras could help us find this answer, the question lacks meaning. Slide ladders don’t form right angles with the ground. The slide ramp doesn’t run all the way to the ground nor is it a straight line; the tail of it curves. Also, if the child can measure the ladder and base, why can’t the ramp be measured as easily? Lastly, what is this child doing playing with a tape measure during recess instead of playing on the slide?
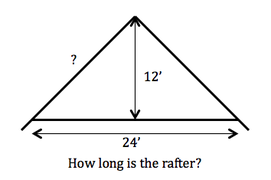
Our task as teachers is to give meaning to the math. There are many ways to do this. Using the previous example, I wanted my students to see how the Pythagorean theorem could really be used. I gave some examples when I used it during the construction of my home. One was when I needed to know the length of the rafters that would form my roof. I couldn’t measure them, as I was writing the lumber bid at the time to apply for the bank loan and needed to know how much lumber to buy; there were no rafters to measure yet. When I explained that by doing this work myself I saved over $30,000 on the construction of my home, they saw the meaning and I had their interest.
The students found this meaningful because they had just completed a science lab on the burning of a candle (the paraffin) and I had made a whoosh rocket just prior; they love fire! When we later studied functions, I reminded them of how they had used these principles to discover the formula for real hydrocarbon fuels.
What really surprises me is how easily I can engage my eighth grade students in the mathematics by something as silly as substituting their names into word problems. I even make the problems nonsense, and they engage even more. Here is an example:
Original word problem:
Painter A can paint a room in 3 hours. Painter B can paint the same room in 2 hours. How long will it take if they work together?
Edited version:
Dylan can wash an aardvark in 3 hours. Celina can wash the same aardvark in 2 hours? How long will it take them to clean their aardvark if they work together?
This problem has no more meaning than the original in the sense that it has little application to the lives of the students. In fact it could be argued that Dylan and Celina are more likely to paint a room than wash an aardvark, yet the students still engage more in the modified problem. I believe our brains are willing to participate in mathematics and backflips and dissections for the simple pleasure of learning whether it has immediate application or not.
So meaning can be direct and practical and real as in the example of building a home and saving money. Meaning can also be defined as any activity that doesn’t seem meaning-less. Our brains’ desire to learn is significant and meaningful in its own right.
As we have ventured through these six factors – respect, recognition, belonging, autonomy, personal growth, and meaning – some conclusions are apparent. First, the needs that drive employees to be productive and successful are the same ones that will foster success in our students. Secondly, it is probably more difficult to develop these conditions in a classroom than it is in the business world. Our limited time and budgets hinder our attempts. However, our students tend to be more resilient and willing than most adults, so even small incremental changes can bring immediate and surprising results.
 RSS Feed
RSS Feed