In the article, Ms. Wiggins listed her top ten reasons for making STEM instruction the foundation for your math and science curriculum.
1. STEM has real world application
2. STEM fosters problem-solving skills
4. STEM is differentiated instruction
5. STEM promotes cooperative learning
6. STEM teaches creativity
7. STEM makes failure a learning opportunity
8. STEM involves high-level thinking
9. STEM requires students to be actively engaged
10. STEM is the future
I agree with her on all counts and would add an eleventh reason that I have encountered as a middle grades STEM teacher. During the coming weeks, we will explore each of Wiggins’ ideas in more depth, and at the end, I will tell you my eleventh reason.
1. STEM connects with real world application
As a math teachers, many of us hear the question, “When are we ever gonna use this?” I have to answer that quite often my honest answer would be, “Never.”
A person asked me the other day, “You are a teacher. Why don’t we teach math the way it used to be taught? Students can’t do the most simple pencil and paper math these days.”
I pulled out my smart phone and showed him the PhotoMath app. “I can point my camera at a math problem and push this button. In less than a second it will display the answer and show the steps. Why would a student need to know how to divide a decimal using long division? Who would hire him or her for that skill? The truth is, in some instances teaching pencil and paper math is like teaching horseshoeing; it once had a value, but it isn’t a job skill anymore. We have to ask ourselves whether we are teaching to their future or our past?”
I then showed him a YouTube video of the robot bugs my students made using electric vibrating toothbrushes from the Dollar Store. (https://www.youtube.com/watch?v=wWl5lH-fMAI) They then had to race their vibrobots down a track and calculate and graph the speed and acceleration. His face lit up. “Now that’s what students should be doing!” he exclaimed.
The real world that my students will encounter when they finish school is not the world in which I grew up. The truth is that if we don’t prepare American students for this reality, we will have to look elsewhere for the high quality workers our society will need.
The textbooks of my past had contrived examples showing how math and science are used in the real world. One book showed two people carrying a sheet of paneling through a doorway. The question asked, “Two carpenters need to carry a sheet of paneling through a doorway that measures one meter wide by two meters tall. What is the longest piece of paneling that will fit through the doorway?” The lesson was clearly suggesting the need to use the Pythagorean theorem to find the diagonal measure of the doorway. It doesn’t take your most clever student to see how fictional this scenario is.
- Doors are all 80 inches tall. There are no two-meter high doors.
- Doors are measured in inches, not meters. This is just an attempt to conform a textbook to the metrics movement.
- All paneling measures 4 feet by 8 feet. There is no question of “what is the longest panel…”
- It only takes one carpenter to carry a sheet of paneling. If a second one is helping, he needs to be fired.
- If you turn the panel sideways, it is only 4 feet wide and will fit through a hobbit’s door.
- No one has used paneling since 1977.
My robotics engineers made their bots with paper clip legs or toothbrush bristle feet. One boy made a bot with tongue depressor skis for feet. The paper clip feet vibrated best and moved more quickly down the track until they got to the sloped part. Then the bristles slid down the track faster due to the lack of friction and the boy with the ski-bot suddenly took the lead!
Friction is involved in both scenarios, but no one needs to understand friction to move a dresser.
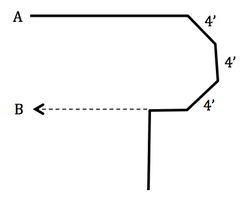
Similarly, I told my students about how I used the Pythagorean theorem in designing and building my house. I have a semi-octagonal porch on one side. Each edge of the octagonal wing is 4 feet long. I had to put a brace in the concrete at point B while the concrete of the porch was being poured. Thus I had to know the exact location of point B before the porch even existed. This required some advanced applications of the theorem to calculate the distance from point A to point B.
During the remainder of my unit on force and motion, I constantly asked students to imagine that they were trying to remotely navigate the Mars Rover. “Can you imagine how challenging it is for the programmers to move the Rover from one location to another and know its exact location when they are on the spinning Earth and trying to give instructions to a craft they can’t see spinning on another planet with a four-minute delay in communication between the two? Can you imagine how difficult it would be to pass the basketball to your teammate during a game if you were both on separate spinning courts and you had to release the ball knowing where your teammate would be four minutes later?”
Wiggins is right; when we ask students to do the problem-based learning encountered in STEM instruction, they encounter real world obstacles, and they learn to conquer them. And after all, isn’t that one of the main reasons we became teachers?
 RSS Feed
RSS Feed